Residual Entropy

The residual entropy, or erasure entropy, is a dual to the Dual Total Correlation. It is dual in the sense that together they form the entropy of the distribution.

\[\begin{split}\R{X_{0:n}} &= \sum \H{X_i | X_{\{0..n\}/i}} \\ &= -\sum_{x_{0:n} \in X_{0:n}} p(x_{0:n}) \log_2 \prod p(x_i|x_{\{0:n\}/i})\end{split}\]

The residual entropy was originally proposed in [VW08] to quantify the information lost by sporatic erasures in a channel. The idea here is that only the information uncorrelated with other random variables is lost if that variable is erased.

If a joint distribution consists of independent random variables, the residual entropy is equal to the Entropy:

In [1]: from dit.multivariate import entropy, residual_entropy

In [2]: d = dit.uniform_distribution(3, 2)

In [3]: entropy(d) == residual_entropy(d)
Out[3]: True

Another simple example is a distribution where one random variable is independent of the others:

In [4]: d = dit.uniform(['000', '001', '110', '111'])

In [5]: residual_entropy(d)
Out[5]: 1.0

If we ask for the residual entropy of only the latter two random variables, the middle one is now independent of the others and so the residual entropy grows:

In [6]: residual_entropy(d, [[1], [2]])
Out[6]: 2.0

Visualization

The residual entropy consists of all the unshared information in the distribution. That is, it is the information in each variable not overlapping with any other.

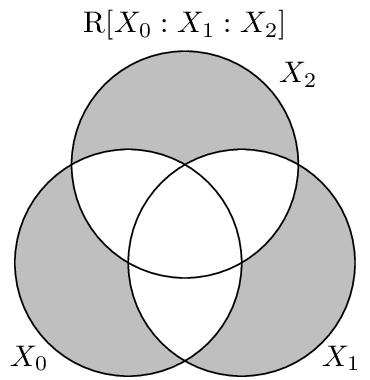
$The residual entropy :math:`\R{X : Y}`$ $The residual entropy :math:`\R{X : Y : Z}`$

API

residual_entropy(dist, rvs=None, crvs=None)[source]

Compute the residual entropy.

Parameters:

dist (Distribution) – The distribution from which the residual entropy is calculated.
rvs (list, None) – The indexes of the random variable used to calculate the residual entropy. If None, then the total correlation is calculated over all random variables.
crvs (list, None) – The indexes of the random variables to condition on. If None, then no variables are condition on.

Returns:

R – The residual entropy.

Return type:

float

Raises:

ditException – Raised if dist is not a joint distribution or if rvs or crvs contain non-existant random variables.