Information Profiles¶
There are several ways to decompose the information contained in a joint distribution. Here, we will demonstrate their behavior using four examples drawn from [ASBY14]:
In [1]: from dit.profiles import *
In [2]: ex1 = dit.Distribution(['000', '001', '010', '011', '100', '101', '110', '111'], [1/8]*8)
In [3]: ex2 = dit.Distribution(['000', '111'], [1/2]*2)
In [4]: ex3 = dit.Distribution(['000', '001', '110', '111'], [1/4]*4)
In [5]: ex4 = dit.Distribution(['000', '011', '101', '110'], [1/4]*4)
Shannon Partition and Extropy Partition¶
The I-diagrams, or ShannonPartition, for these four examples can be computed thusly:
In [6]: ShannonPartition(ex1)
Out[6]:
+----------+--------+
| measure | bits |
+----------+--------+
| H[0|1,2] | 1.000 |
| H[1|0,2] | 1.000 |
| H[2|0,1] | 1.000 |
| I[0:1|2] | 0.000 |
| I[0:2|1] | 0.000 |
| I[1:2|0] | 0.000 |
| I[0:1:2] | 0.000 |
+----------+--------+
In [7]: ShannonPartition(ex2)
Out[7]:
+----------+--------+
| measure | bits |
+----------+--------+
| H[0|1,2] | 0.000 |
| H[1|0,2] | 0.000 |
| H[2|0,1] | 0.000 |
| I[0:1|2] | 0.000 |
| I[0:2|1] | 0.000 |
| I[1:2|0] | 0.000 |
| I[0:1:2] | 1.000 |
+----------+--------+
In [8]: ShannonPartition(ex3)
Out[8]:
+----------+--------+
| measure | bits |
+----------+--------+
| H[0|1,2] | 0.000 |
| H[1|0,2] | 0.000 |
| H[2|0,1] | 1.000 |
| I[0:1|2] | 1.000 |
| I[0:2|1] | 0.000 |
| I[1:2|0] | 0.000 |
| I[0:1:2] | 0.000 |
+----------+--------+
In [9]: ShannonPartition(ex4)
Out[9]:
+----------+--------+
| measure | bits |
+----------+--------+
| H[0|1,2] | 0.000 |
| H[1|0,2] | 0.000 |
| H[2|0,1] | 0.000 |
| I[0:1|2] | 1.000 |
| I[0:2|1] | 1.000 |
| I[1:2|0] | 1.000 |
| I[0:1:2] | -1.000 |
+----------+--------+
And their X-diagrams, or ExtropyDiagram, can be computed like so:
In [10]: ExtropyPartition(ex1)
Out[10]:
+----------+--------+
| measure | exits |
+----------+--------+
| X[0|1,2] | 0.103 |
| X[1|0,2] | 0.103 |
| X[2|0,1] | 0.103 |
| X[0:1|2] | 0.142 |
| X[0:2|1] | 0.142 |
| X[1:2|0] | 0.142 |
| X[0:1:2] | 0.613 |
+----------+--------+
In [11]: ExtropyPartition(ex2)
Out[11]:
+----------+--------+
| measure | exits |
+----------+--------+
| X[0|1,2] | 0.000 |
| X[1|0,2] | 0.000 |
| X[2|0,1] | 0.000 |
| X[0:1|2] | 0.000 |
| X[0:2|1] | 0.000 |
| X[1:2|0] | 0.000 |
| X[0:1:2] | 1.000 |
+----------+--------+
In [12]: ExtropyPartition(ex3)
Out[12]:
+----------+--------+
| measure | exits |
+----------+--------+
| X[0|1,2] | 0.000 |
| X[1|0,2] | 0.000 |
| X[2|0,1] | 0.245 |
| X[0:1|2] | 0.245 |
| X[0:2|1] | 0.000 |
| X[1:2|0] | 0.000 |
| X[0:1:2] | 0.755 |
+----------+--------+
In [13]: ExtropyPartition(ex4)
Out[13]:
+----------+--------+
| measure | exits |
+----------+--------+
| X[0|1,2] | 0.000 |
| X[1|0,2] | 0.000 |
| X[2|0,1] | 0.000 |
| X[0:1|2] | 0.245 |
| X[0:2|1] | 0.245 |
| X[1:2|0] | 0.245 |
| X[0:1:2] | 0.510 |
+----------+--------+
Complexity Profile¶
The complexity profile, implimented by ComplexityProfile is simply the amount of information at scale \(\geq k\) of each “layer” of the I-diagram [BY04].
Consider example 1, which contains three independent bits. Each of these bits are in the outermost “layer” of the i-diagram, and so the information in the complexity profile is all at layer 1:
In [14]: ComplexityProfile(ex1).draw();

Whereas in example 2, all the information is in the center, and so each scale of the complexity profile picks up that one bit:
In [15]: ComplexityProfile(ex2).draw();

Both bits in example 3 are at a scale of at least 1, but only the shared bit persists to scale 2:
In [16]: ComplexityProfile(ex3).draw();

Finally, example 4 (where each variable is the exclusive or of the other two):
In [17]: ComplexityProfile(ex4).draw();

Marginal Utility of Information¶
The marginal utility of information (MUI) [ASBY14], implimented by MUIProfile takes a different approach. It asks, given an amount of information \(\I{d : \left\{X\right\}} = y\), what is the maximum amount of information one can extract using an auxilliary variable \(d\) as measured by the sum of the pairwise mutual informations, \(\sum \I{d : X_i}\). The MUI is then the rate of this maximum as a function of \(y\).
For the first example, each bit is independent and so basically must be extracted independently. Thus, as one increases \(y\) the maximum amount extracted grows equally:
In [18]: MUIProfile(ex1).draw();

In the second example, there is only one bit total to be extracted, but it is shared by each pairwise mutual information. Therefore, for each increase in \(y\) we get a threefold increase in the amount extracted:
In [19]: MUIProfile(ex2).draw();

For the third example, for the first one bit of \(y\) we can pull from the shared bit, but after that one must pull from the independent bit, so we see a step in the MUI profile:
In [20]: MUIProfile(ex3).draw();

Lastly, the xor example:
In [21]: MUIProfile(ex4).draw();

Schneidman Profile¶
Also known as the connected information or network informations, the Schneidman profile (SchneidmanProfile) exposes how much information is learned about the distribution when considering \(k\)-way dependencies [Ama01][SSB+03]. In all the following examples, each individual marginal is already uniformly distributed, and so the connected information at scale 1 is 0.
In the first example, all the random variables are independent already, so fixing marginals above \(k=1\) does not result in any change to the inferred distribution:
In [22]: SchneidmanProfile(ex1).draw();

In the second example, by learning the pairwise marginals, we reduce the entropy of the distribution by two bits (from three independent bits, to one giant bit):
In [23]: SchneidmanProfile(ex2).draw();

For the third example, learning pairwise marginals only reduces the entropy by one bit:
In [24]: SchneidmanProfile(ex3).draw();

And for the xor, all bits appear independent until fixing the three-way marginals at which point one bit about the distribution is learned:
In [25]: SchneidmanProfile(ex4).draw();

Entropy Triangle and Entropy Triangle2¶
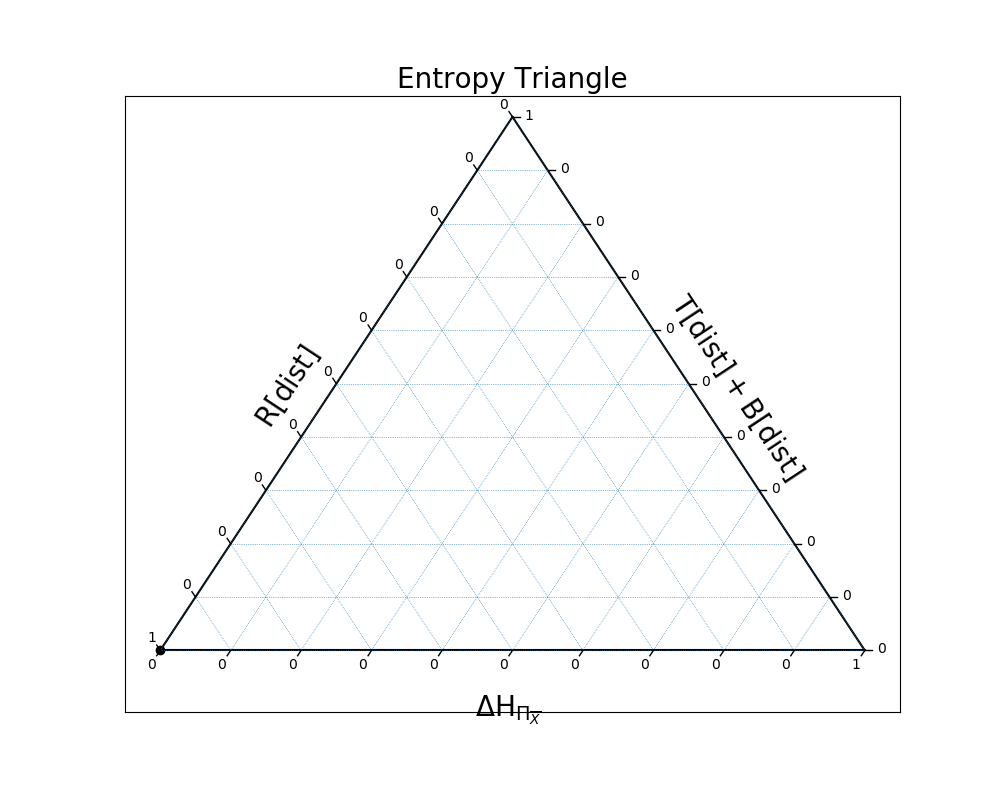
The entropy triangle, EntropyTriangle, [VAPelaezM16] is a method of visualizing how the information in the distribution is distributed among deviation from uniformity, independence, and dependence. The deviation from independence is measured by considering the difference in entropy between a independent variables with uniform distributions, and independent variables with the same marginal distributions as the distribution in question. Independence is measured via the Residual Entropy, and dependence is measured by the sum of the Total Correlation and Dual Total Correlation.
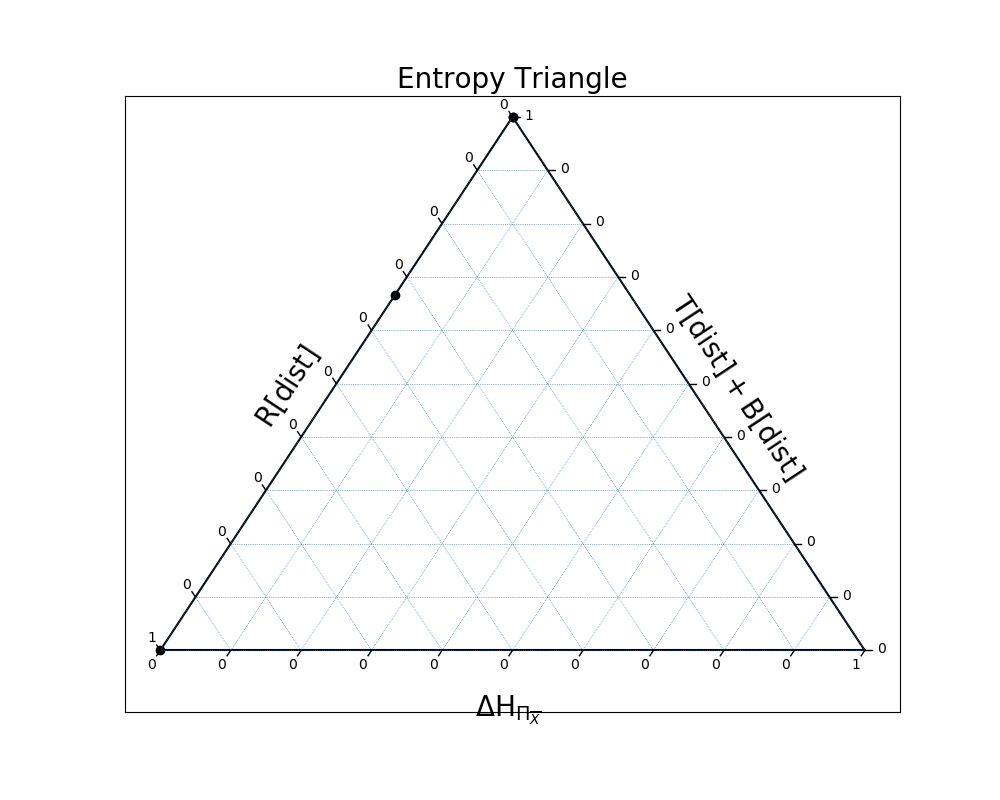
All four examples lay along the left axis because their distributions are uniform over the events that have non-zero probability.
In the first example, the distribution is all independence because the three variables are, in fact, independent:
In [26]: EntropyTriangle(ex1).draw();
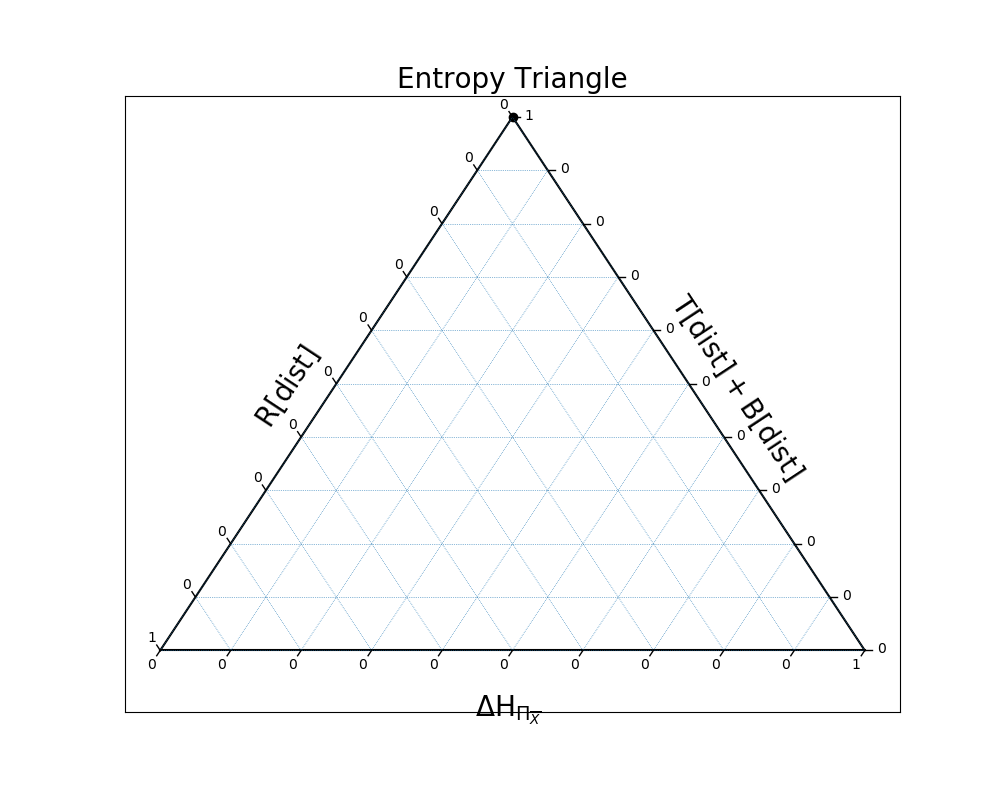
In the second example, the distribution is all dependence, because the three variables are perfectly entwined:
In [27]: EntropyTriangle(ex2).draw();
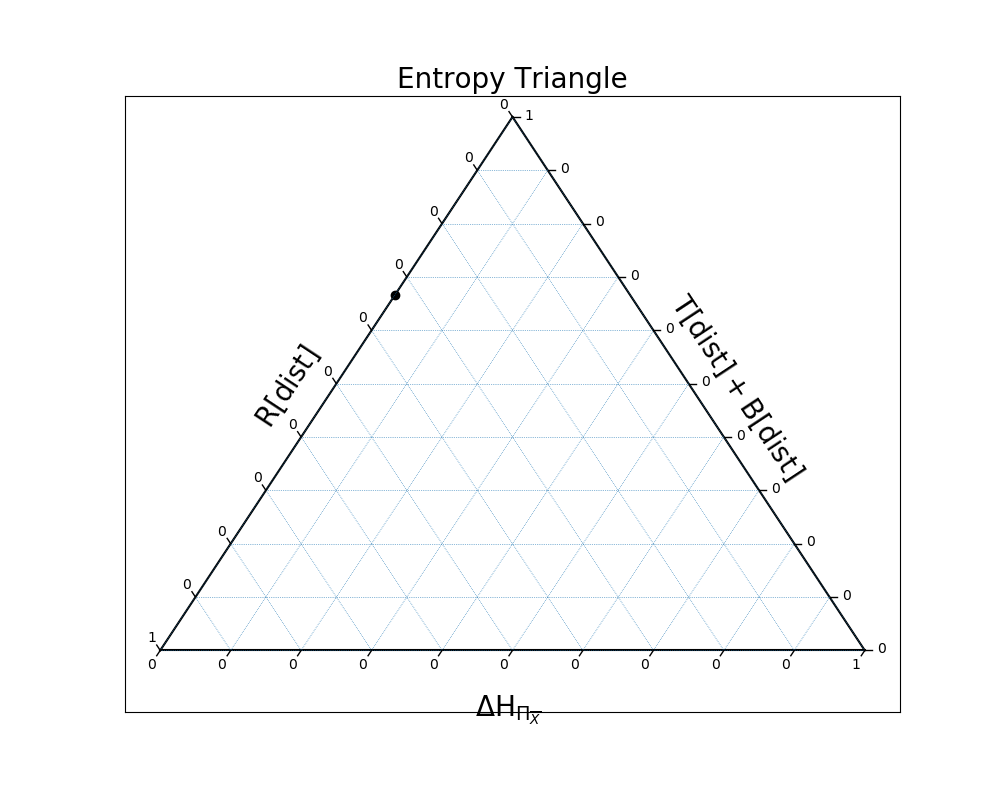
Here, there is a mix of independence and dependence:
In [28]: EntropyTriangle(ex3).draw();
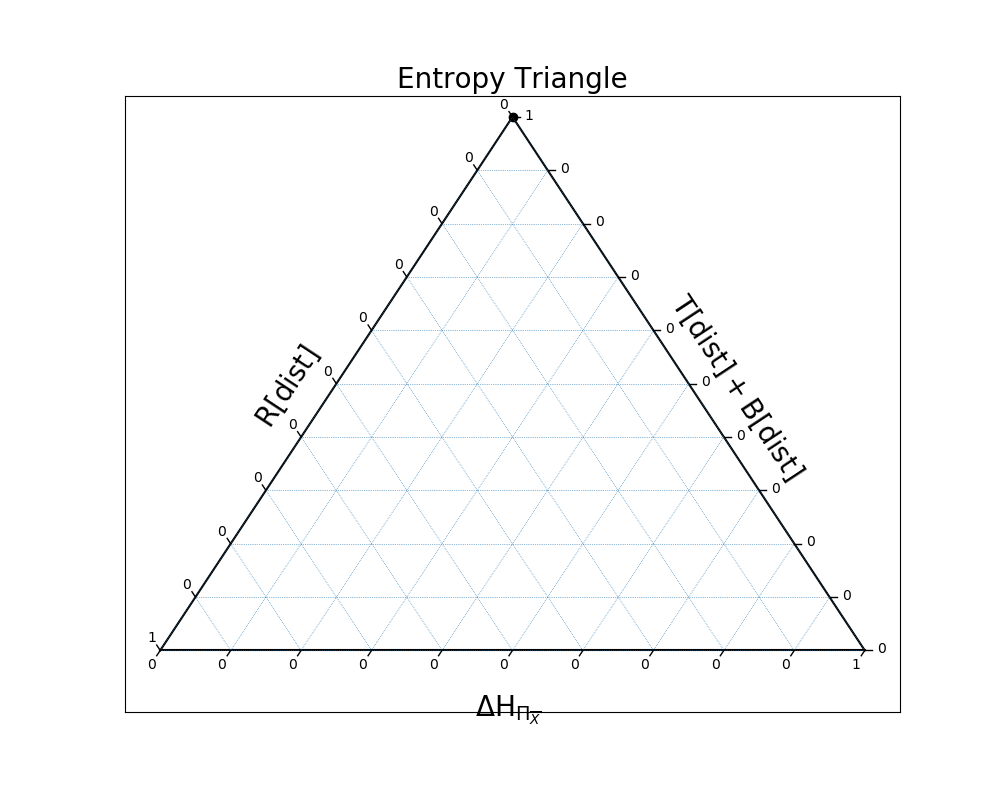
And finally, in the case of xor, the variables are completely dependent again:
In [29]: EntropyTriangle(ex4).draw();
We can also plot all four on the same entropy triangle:
In [30]: EntropyTriangle([ex1, ex2, ex3, ex4]).draw();
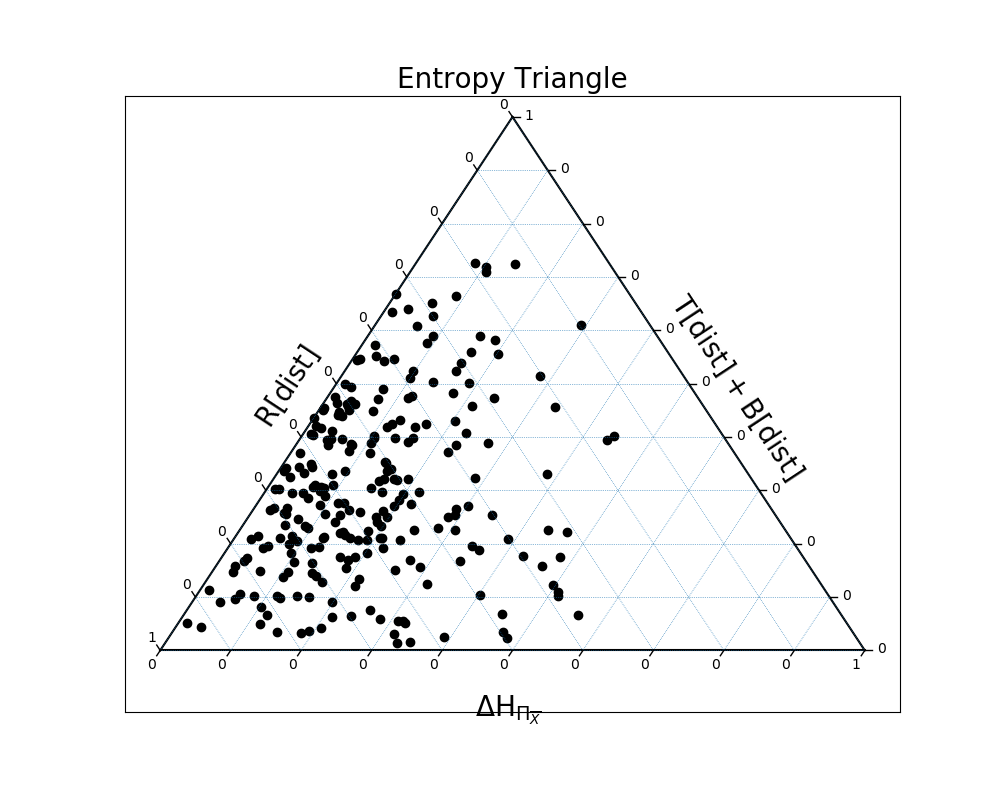
In [31]: dists = [ dit.random_distribution(3, 2, alpha=(0.5,)*8) for _ in range(250) ]
In [32]: EntropyTriangle(dists).draw();
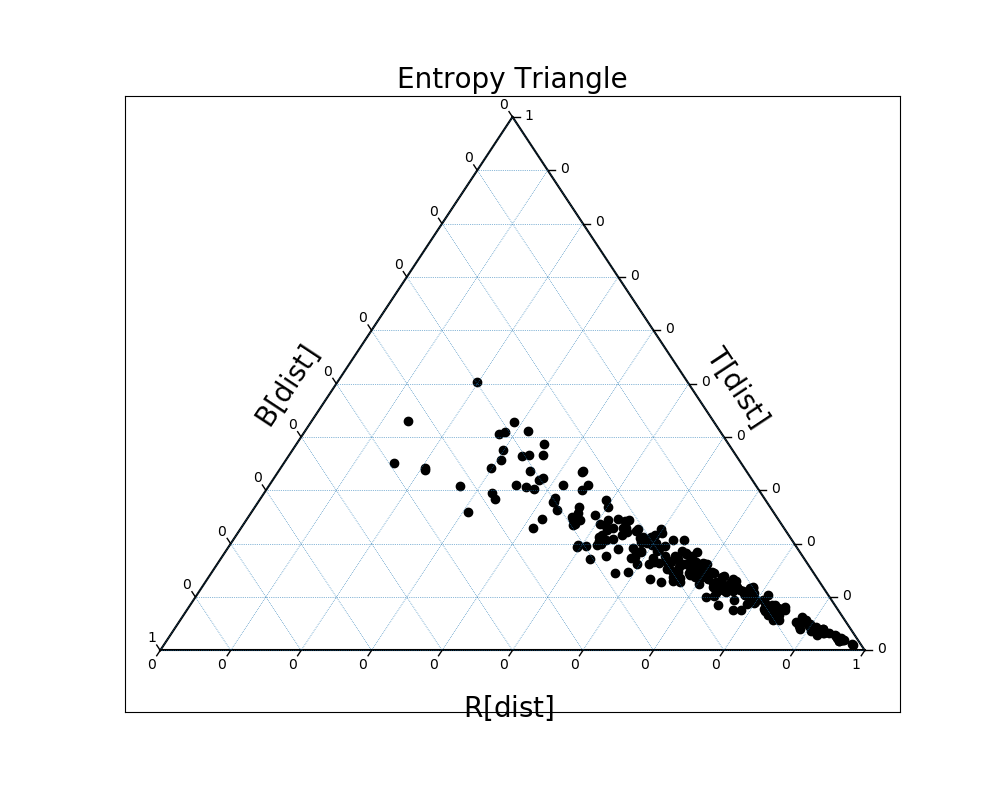
We can plot these same distributions on a slightly different entropy triangle as well, EntropyTriangle2, one comparing the Residual Entropy, Total Correlation, and Dual Total Correlation:
In [33]: EntropyTriangle2(dists).draw();
Dependency Decomposition¶
Using DependencyDecomposition, one can discover how an arbitrary information measure varies as marginals of the distribution are fixed. In our first example, each variable is independent of the others, and so constraining marginals makes no difference:
In [34]: DependencyDecomposition(ex1)
Out[34]:
+------------+--------+
| dependency | H |
+------------+--------+
| 012 | 3.000 |
| 01:02:12 | 3.000 |
| 01:02 | 3.000 |
| 01:12 | 3.000 |
| 02:12 | 3.000 |
| 01:2 | 3.000 |
| 02:1 | 3.000 |
| 12:0 | 3.000 |
| 0:1:2 | 3.000 |
+------------+--------+
In the second example, we see that fixing any one of the pairwise marginals reduces the entropy by one bit, and by fixing a second we reduce the entropy down to one bit:
In [35]: DependencyDecomposition(ex2)
Out[35]:
+------------+--------+
| dependency | H |
+------------+--------+
| 012 | 1.000 |
| 01:02:12 | 1.000 |
| 01:02 | 1.000 |
| 01:12 | 1.000 |
| 02:12 | 1.000 |
| 01:2 | 2.000 |
| 02:1 | 2.000 |
| 12:0 | 2.000 |
| 0:1:2 | 3.000 |
+------------+--------+
In the third example, only constraining the 01 marginal reduces the entropy, and it reduces it by one bit:
In [36]: DependencyDecomposition(ex3)
Out[36]:
+------------+--------+
| dependency | H |
+------------+--------+
| 012 | 2.000 |
| 01:02:12 | 2.000 |
| 01:02 | 2.000 |
| 01:12 | 2.000 |
| 02:12 | 3.000 |
| 01:2 | 2.000 |
| 02:1 | 3.000 |
| 12:0 | 3.000 |
| 0:1:2 | 3.000 |
+------------+--------+
And finally in the case of the exclusive or, only constraining the 012 marginal reduces the entropy.
In [37]: DependencyDecomposition(ex4)
Out[37]:
+------------+--------+
| dependency | H |
+------------+--------+
| 012 | 2.000 |
| 01:02:12 | 3.000 |
| 01:02 | 3.000 |
| 01:12 | 3.000 |
| 02:12 | 3.000 |
| 01:2 | 3.000 |
| 02:1 | 3.000 |
| 12:0 | 3.000 |
| 0:1:2 | 3.000 |
+------------+--------+