Rate Distortion Theory¶
Note
We use \(p\) to denote fixed probability distributions, and \(q\) to denote probability distributions that are optimized.
Rate-distortion theory [CT06] is a framework for studying optimal lossy compression. Given a distribution \(p(x)\), we wish to find \(q(\hat{x}|x)\) which compresses \(X\) as much as possible while limiting the amount of user-defined distortion, \(d(x, \hat{x})\). The minimum rate (effectively, code book size) at which \(X\) can be compressed while maintaining a fixed distortion is known as the rate-distortion curve:
By introducing a Lagrange multiplier, we can transform this constrained optimization into an unconstrained one:
where minimizing at each \(\beta\) produces a point on the curve.
Example¶
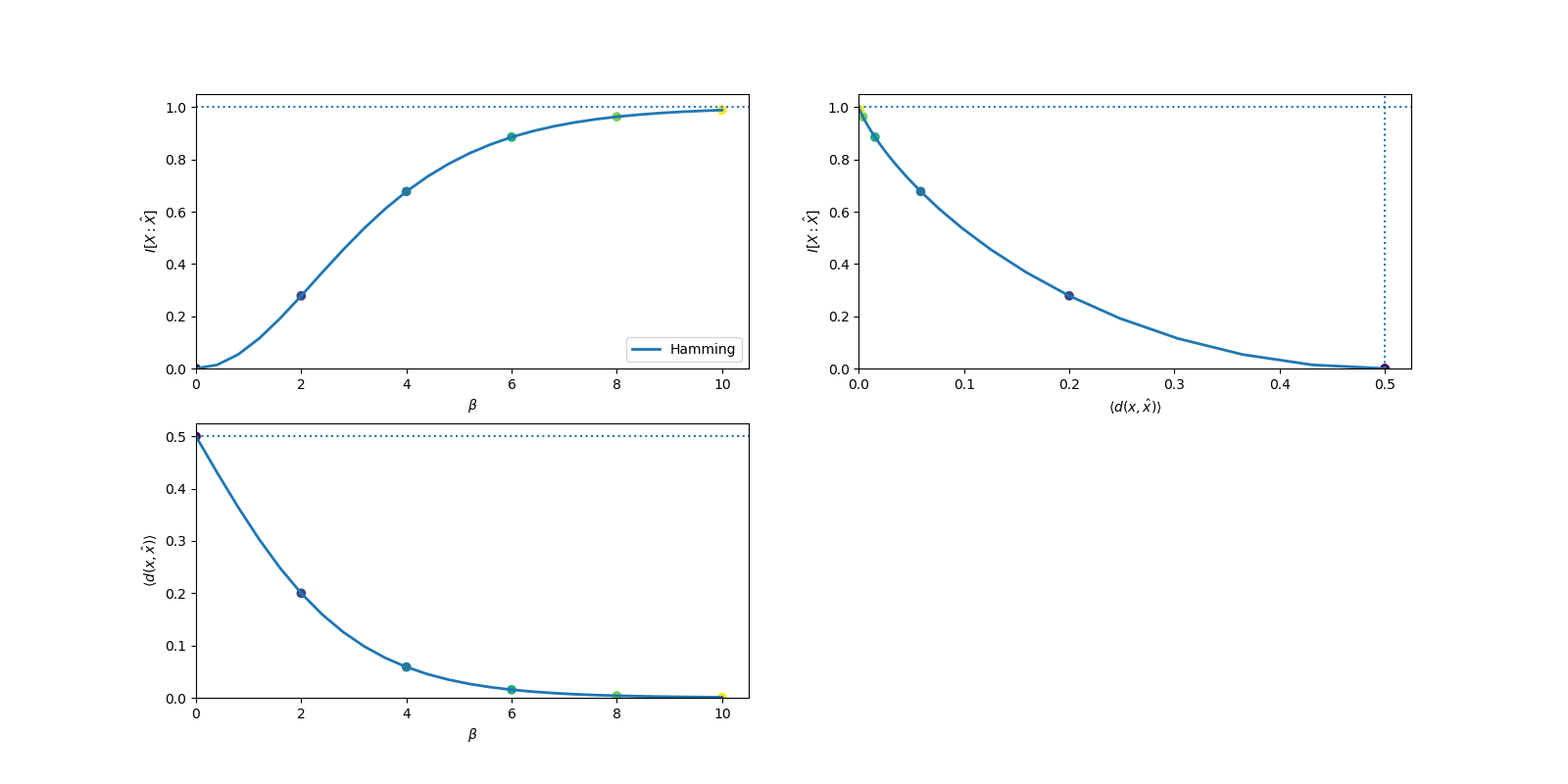
It is known that under the Hamming distortion (\(d(x, \hat{x}) = \left[ x \neq \hat{x} \right]\)) the rate-distortion function for a biased coin has the following solution: \(R(D) = \H{p} - \H{D}\):
In [1]: from dit.rate_distortion import RDCurve
In [2]: d = dit.Distribution(['0', '1'], [1/2, 1/2])
In [3]: RDCurve(d, beta_num=26).plot();
Information Bottleneck¶
The information bottleneck [TPB00] is a form of rate-distortion where the distortion measure is given by:
where \(D\) is an arbitrary divergence measure, and \(\hat{X} - X - Y\) form a Markov chain. Traditionally, \(D\) is the Kullback-Leibler Divergence, in which case the average distortion takes a particular form:
Since \(\I{X : Y}\) is constant over \(q(\hat{x} | x)\), it can be removed from the optimization. Furthermore,
where the final equality is due to the Markov chain. Due to all this, Information Bottleneck utilizes a “relevance” term, \(\I{\hat{X} : Y}\), which replaces the average distortion in the Lagrangian:
Though \(\I{X : Y | \hat{X}}\) is the most simplified form of the average distortion, it is faster to compute \(\I{\hat{X} : Y}\) during optimization.
Example¶
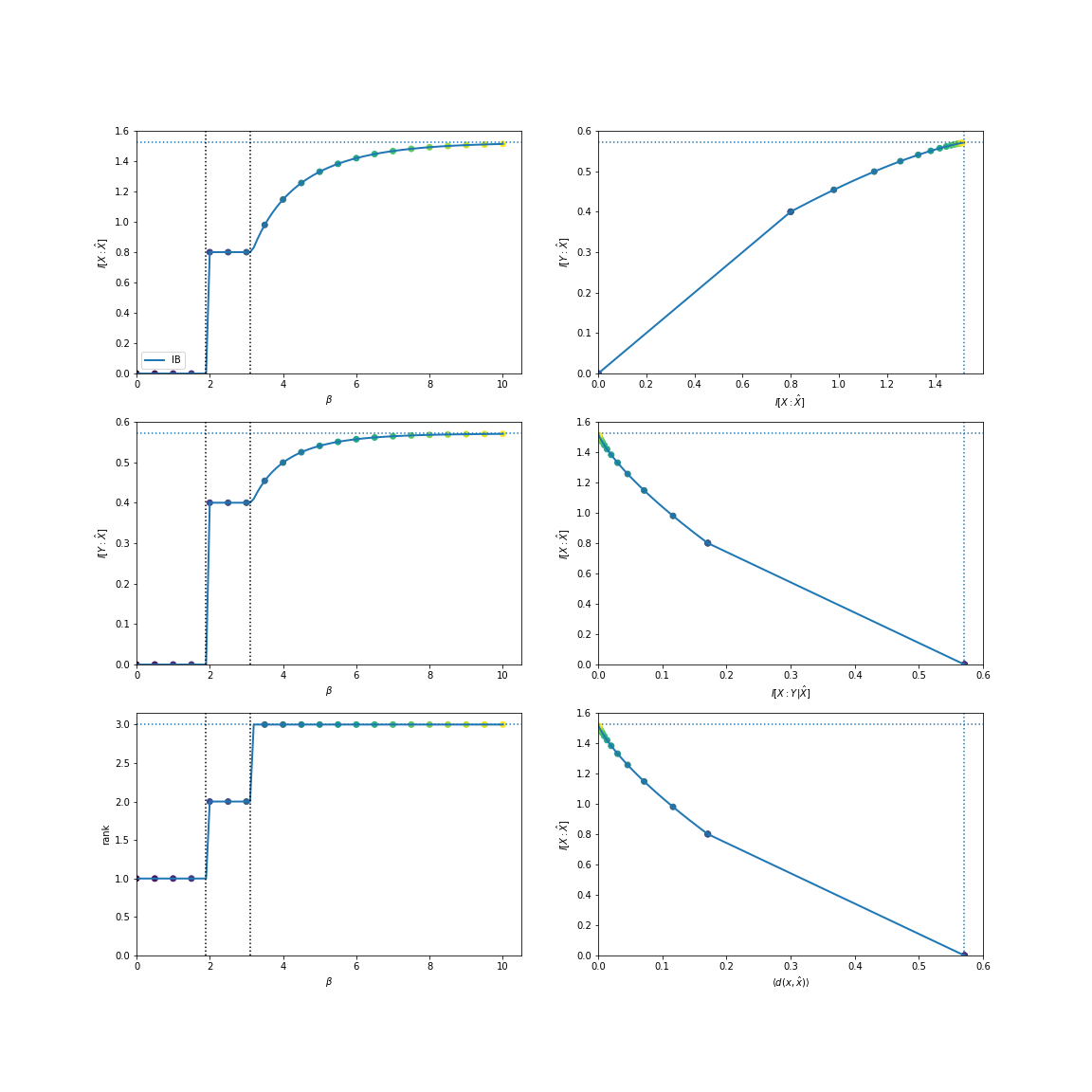
Consider this distribution:
In [4]: d = dit.Distribution(['00', '02', '12', '21', '22'], [1/5]*5)
There are effectively three features that the fist index, \(X\), has regarding the second index, \(Y\). We can find them using the standard information bottleneck:
In [5]: from dit.rate_distortion import IBCurve
In [6]: IBCurve(d, beta_num=26).plot();
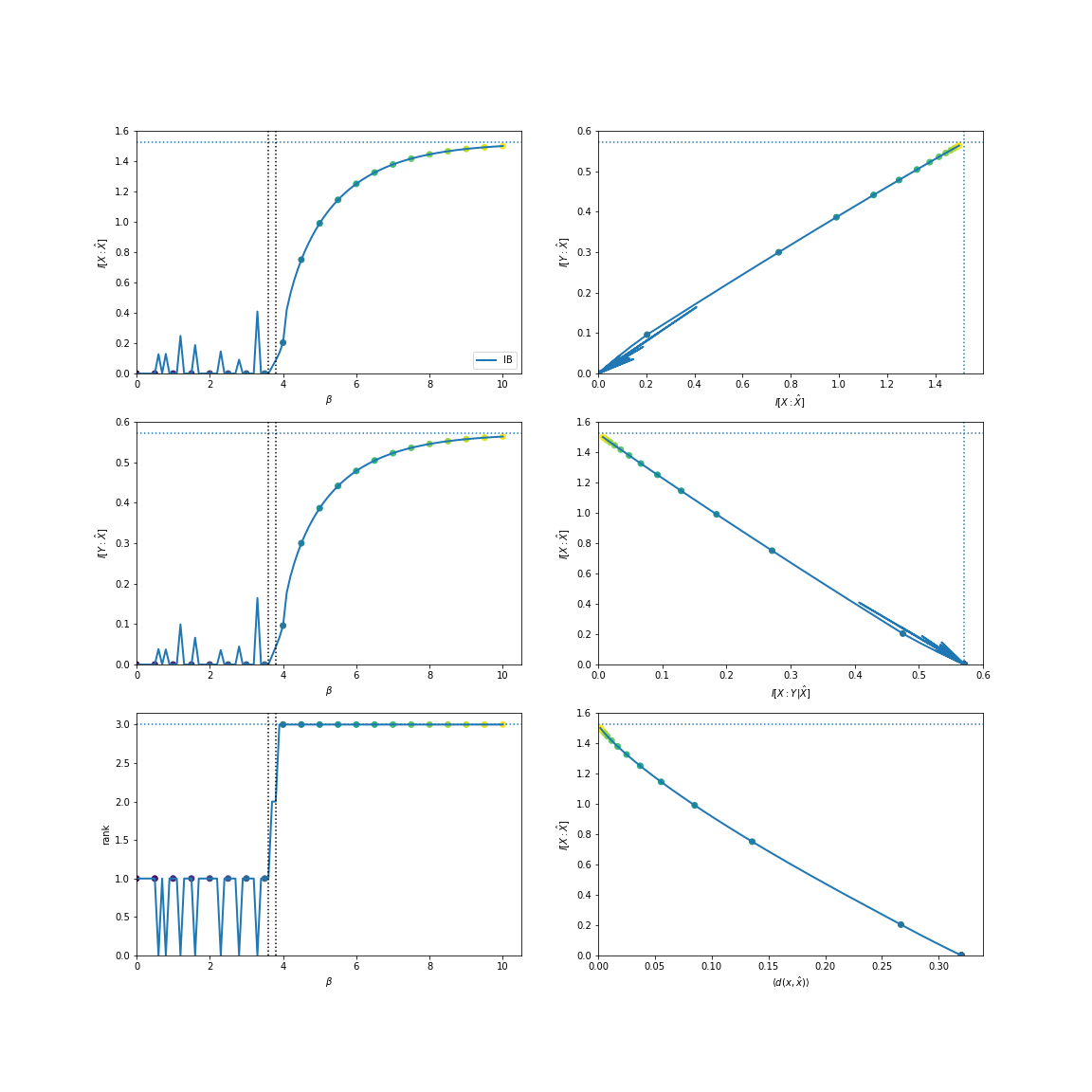
We can also find them utilizing the total variation:
In [7]: from dit.divergences.pmf import variational_distance
In [8]: IBCurve(d, divergence=variational_distance).plot();
Note
The spiky behavior at low \(\beta\) values is due to numerical imprecision.
APIs¶
-
class
RDCurve(dist, rv=None, crvs=None, beta_min=0, beta_max=10, beta_num=101, alpha=1.0, distortion=Distortion(name='Hamming', matrix=<function hamming_distortion>, optimizer=<class 'dit.rate_distortion.rate_distortion.RateDistortionHamming'>), method=None)[source]¶ Compute a rate-distortion curve.